Deep Learning in Zeitreihenvorhersagen

Richtig eingesetzt können Methodiken aus dem Gebiet der Data Science einen wirklichen Mehrwert für die Anforderungen von Unternehmen liefern. Wo früher einfach Reporting-Lösungen den Blick in die Vergangenheit boten, können statistische Methoden in Kombination mit künstlicher Intelligenz sehr viel mehr leisten.

Wenn man sich einmal die historische Entwicklung und die damit einhergehende technologische Veränderung betrachtet, wird klar, dass Machine Learning die Brücke in die Zukunft ist. Maschinelles Lernen ist ein Gebiet der Informationstechnik, das in den letzten zehn Jahren an Fortschritt und Popularität enorm zunahm. 1952 wurde Arthur Samuel gefeiert, dessen selbstlernender Algorithmus das Brettspiel Dame erlernte. Inzwischen muss sich die Gesellschaft mit Grundsatzfragen nach autonom fahrenden Autos beschäftigen.

Allein diese Betrachtung zeigt Ihnen bereits auf, welch umfassenden Einsatzgebiete und Möglichkeiten maschinelles Lernen haben kann. Mit unterschiedlichsten Ansätzen, die im Groben in zwei Problembereiche — Regression und Klassifikation — eingeteilt werden können, werden so bestehende Fragestellungen im geschäftlichen Rahmen behandelt:

• „Was sind meine wertvollsten Kunden?“

• „Welche Preisanpassungen sind im Energieversorgungssektor auf der Basis von Angebot und Nachfrage vorzunehmen?“

• „Was ist der optimale Lagerbestand unserer Vertriebsstätten bzgl. des Standortes?“

Die Grundlage zur Beantwortung all dieser Fragen ist schlicht und ergreifend: Daten.

Zeitreihen

Eine spezielle Datenform sind Zeitreihen (zeitlich aufgelöste Datenpunktreihen) und deren Untersuchung stellt ein Spezialgebiet der Regressionsanalyse dar. Die Analyse dieser Objekte und das Treffen von Vorhersagen auf deren Basis ist für viele Industrien und technologischen Anwendungen von großem Interesse.

Zunächst: Was sind Zeitreihen? Eine Definition besagt, dass es sich um quantitative Beobachtungen handelt, die in zeitlich regelmäßigen Abständen nacheinander gemessen werden. Dazu gehören die kontinuierliche Herzfrequenzmessung eines Patienten, die Aktienpreise einer Firma zum Ende eines jeden Börsentages oder der monatliche bzw. jährliche Energieverbrauch pro Kopf in einem Regionalgebiet.

Ein Beispiel zur Abbildung der Anzahl Sonnenflecken auf der Zeitachse.

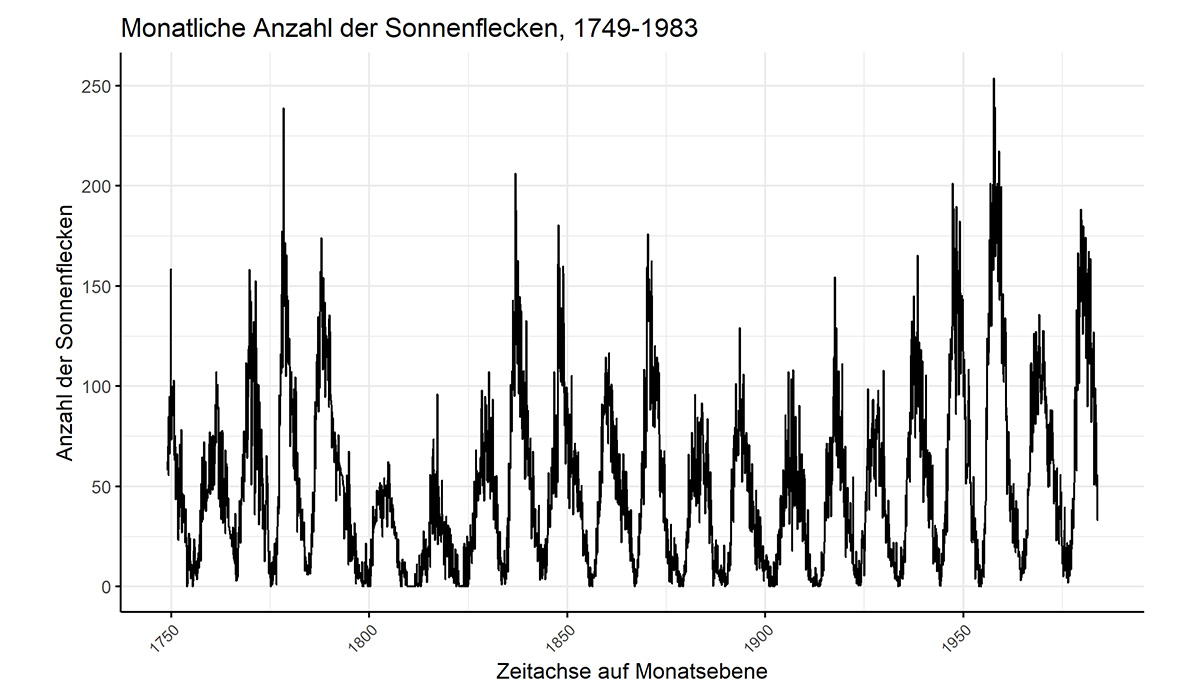
Für diese Datenmengen und die oben erwähnten Fragestellungen existiert ein Füllhorn von statistischen Vorhersagemethoden.

Erläuterung der Methoden

Je nach Anwendungsfall können SARIMA-Modelle (Seasonal Autoregressive Integrated Moving Average) herangezogen werden, die annehmen, dass der zukünftige Wert von den vorangegangenen Werten (Stichwort: autoregressiv) und nicht-stationären Eigenschaften abhängt. Während Saisonalität noch eine allgemeinbekannte Bedeutung hat, ist die Stationarität ein eher unbekanntes Konzept. Darunter ist eine wichtige Eigenschaft von Zeitreihen zu verstehen, die für statistische Modelle gewünscht wird. Es heißt eine Zeitreihe ist stationär, wenn ihre statistischen Eigenschaften mit der Zeit gleichbleibend sind. Durchschnitt und Varianz bleiben also zeitlich erhalten, Kovarianzen sind zeitlich unabhängig. Desweiteren kann auch der Einfluss unterschiedlich lang vergangener Ereignisse mit in ein Modell genommen werden. Exponentielle Glättung (Exponential Smoothing) als ein solches versieht Werte, die weiter entfernt von dem gegenwärtigen Wert liegen, mit einer niedrigeren Gewichtung. Naivere Methoden geben als nächsten Wert in der Zeitreihe den Durchschnitt der letzten p Werte an, optional erweiterbar mit einem Trend und/oder einer Saisonalität. Erwähnenswert ist noch der Unterschied zwischen univariaten und multivariaten Fragestellungen. Univariate Zeitreihen umfassen eine abhängige Variable, zum Beispiel die Temperatur in einer Wettervorhersage, und eine unabhängige Variable, hier der Zeitpunkt der Messung. Erweitern wir unsere Beobachtungen um weitere unabhängige Variablen (Windgeschwindigkeit, Taupunkt, Luftfeuchtigkeit, Grad der Bewölkung, …), so handelt es sich um eine multivariate Zeitreihe. Die gängigste klassische Methode zur Vorhersage von Zeitreihenwerten stellt das vektorautoregressive Modell (VAR) dar. Jede Variable ist eine lineare Funktion, bestehend aus ihren vergangenen sowie den vergangenen Werten aller anderen Variablen.

Und wie können diese Methoden nun helfen?

Selbst mit diesem kleinen Einblick in die Vorhersage mit Hilfe von Zeitreihenanalysen bekommen wir das Gefühl, dass bereits genügend Methoden existieren, um Probleme aus zahlreichen Industrien zufriedenstellend zu lösen. Weshalb sollten praktizierende Datenwissenschaftler dann die Hinzunahme von Deep Learning in ihr Toolkit trotzdem in Erwägung ziehen? Allgemein betrachtet schnitten Deep Learning Methoden nämlich im Vergleich zu klassischen Zeitreihenansätzen bei univariaten Problemstellungen häufig schlechter ab. Nichtsdestotrotz gibt es praktische Gründe für ihre Berücksichtigung. Hierzu vorerst ein kurzer Einblick in die Bereiche des maschinellen Lernens und in fundamentale Konzepte neuronaler Netzwerke.

Maschinelles Lernen kann in drei rudimentäre, sich teils überlappende Bereiche unterteilt werden. Überwachtes Lernen, nicht-überwachtes Lernen und dem Bereich semi-überwachtes bzw. tiefes Lernen. Überwachtes Lernen beschreibt das Finden von Merkmalen (Features), welche an ein Model übergeben werden und das eine Abbildung zwischen eingegebenen und ausgegebenen Daten lernt. Es kann für Regressions- und Klassifikationsprobleme verwendet werden. Nicht-überwachtes Lernen befasst sich mit unbeschrifteten Daten, die es entweder zu Klassifizieren und/oder in sogenannte Cluster (Anhäufungen) zu gruppieren gilt, um etwaige Gemeinsamkeiten oder Unterschiede zu entdecken. Deep Learning als primär interessanter Bereich widmet sich zur Findung von Methoden zur automatischen Erlernung von Merkmalen. Neuronale Netze bekommen Eingabedaten in Form von Vektoren, um diese mit Hilfe geeigneter Operationen aus der linearen Algebra in die vorgegebene Ausgabe (Output) zu transformiert. Mit Hilfe einer Verlustfunktion (Loss Function) wird dann evaluiert, ob die Transformationen zu dem gewünschten Ergebnis führen. Iterativ findet das Model dann mit der Minimierung der Verlustfunktion zu einem Satz geeigneter Merkmale. Folgende intrinsische Eigenschaften machen neuronale Netze so interessant für unser Vorhersageproblem:

1. Sie können willkürliche Abbildungen von Eingabe- und Ausgabedaten lernen.

2. Sie unterstützen mehrfache Ein- und Ausgaben.

3. Sie können automatisch Muster aus langreihigen Eingabedaten lernen (Sehr wichtig für uns!)

Und weshalb ist Deep Learning ein valider Ansatz für Vorhersagen auf Zeitreihenbasis?

Zeitreihen sind eine spezielle Art von Daten, die die Zeit nicht nur als eine Metrik mitnehmen, sondern als eigenständige Dimension. Dies führt dazu, dass eine gesonderte Behandlung der Daten vorgenommen werden muss, denn sie stellen eine zusätzliche Informationsquelle, aber auch eine Einschränkung dar. Wie können neuronale Netze hierbei behilflich sein? Ganz einfach durch das automatische Lernen und Extrahieren von Merkmalen aus rohen und fehlerhaften Daten. Drastische Maßnahmen im Feature Engineering (ein Prozeß zur Erstellung besserer Merkmale für das Model), Datenskalierungen und die Differenzierung für den Erhalt stationärer Zeitreihen ist nicht mehr notwendig. Es ergibt sich also eine große Zeitersparnis und das nicht nur in der Findung geeigneter Merkmale, sondern auch geeigneter Hyperparameter. Ein gängiges Merkmal in der Zeitreihenvorhersage stellt der Lag (Wert zu einem Zeitpunkt in der Vergangenheit) dar, welcher normalerweise durch subjektive Betrachtung des Datenwissenschaftlers festgelegt wird. Menschliche Verzerrung des Modellierungsprozesses wird somit ebenfalls eliminiert. Zusätzlich werden stark gestörte oder nur wenig zusammenhängende Zeitreihen aus Sensordaten (IoT) besser gehandhabt. Klassische Methoden setzen zudem einen linearen Zusammenhang und feste zeitliche Abhängigkeiten zwischen den Variablen voraus, wodurch komplexere und damit interessantere Zusammenhänge gänzlich vernachlässigt werden.

Convolutional Neural Networks

Convolutional Neural Networks (CNNs) sind eine Klasse von neuronalen Netzwerken, die sich als besonders effektiv im automatischen Lernen und Extrahieren von Merkmalen aus rohen Daten erwiesen.

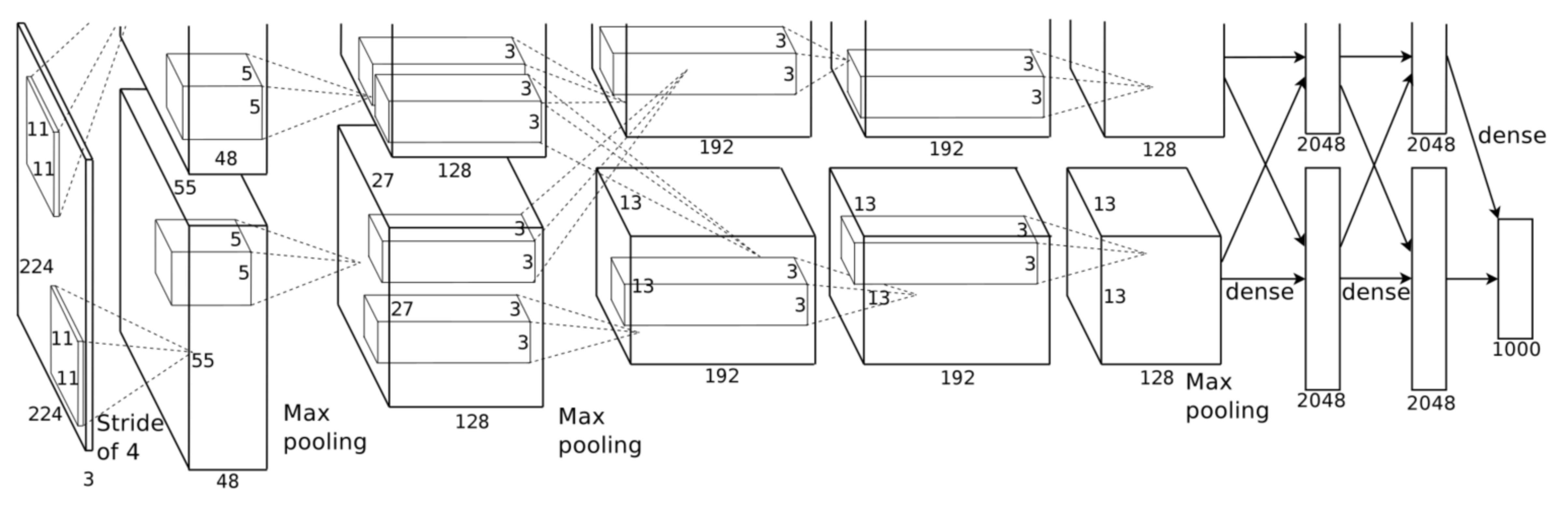
Illustration einer CNN-Architektur. Zwei GPU-Einheiten extrahieren hier unabhängig voneinander Features aus dem zweidimensionalen Datensatz und interagieren nur in bestimmten Ebenen miteinander.

Wie auch in der Bilderkennung und -klassifikation, wo CNNs ihr Hauptanwendungsgebiet wiederfinden, werden die Zeitreihen wie ein eindimensionales Bild eingelesen. Daraufhin werden die direkt nutzbaren Merkmale automatisch identifiziert. Dieser effektive Prozess wird auch als repräsentatives Lernen bezeichnet. Zusätzlich geschieht das unabhängig von der Art und Weise wie die Merkmale in Daten vorkommen, weshalb sie als invariant gegen Transformation bzw. verzerrungsinvariant bezeichnet werden. Für die Zeitreihenklassifikation konnten CNNs bereits vielversprechend eingesetzt werden. In einem Versuch, Ort und Bewegung von Subjekten innerhalb eines Gebäudes auf Zeitreihendaten auf Basis von kabellosen Sensorstärkedaten vorherzusagen, konnten bemerkenswerte Ergebnisse erzielt werden.

Deep Learning für multiple Ein- und Ausgabedaten

Ein weiterer Vorteil von Deep Learning-Ansätzen liegt in der Verarbeitung und Ausgabe multipler Eingabe- und Ausgabedaten. Damit können neben multivariaten Datensätzen auch mehrschrittige Vorhersagemethoden implementiert werden. Das hat zwei Hauptansätze zur Folge:

1. direkt: seperate Modelle werden für jeden Vorhersagezeitpunkt entwickelt

2. rekursiv: ein einzelnes Model wird für einschrittige Vorhersagen verwendet, dessen Ausgabe als neue Eingabe für den nächsten Vorhersagezeitpunkt eingeführt

Für kurze und zusammenhängende Vorhersageblöcke eignet sich der rekursive Ansatz, wohingegen bei unzusammenhängenden Vorhersageblöcken der direkte Ansatz als geeignete Methode bevorzugt wird. Auch eine Mischung aus zusammenhängenden und nicht zusammenhängenden Vorhersageblöcken ist mit dem direkten Ansatz besser zu handhaben. Für Deep Learning-Ansätze ist die Wahl mehrfach gewählter Dateneingaben von kritischem Wert für den Erfolg des Models. Lag-Daten der Zielvariable, multivariate Lag-Daten anderer Variablen und Metadaten über die Zeitvariable führen zu einer geeigneten gelernten Abbildung von den Eingabe- auf die Ausgabedaten.

Neben CNNs gibt es noch eine weitere Klasse neuronaler Netzwerke, die erst mit ansteigender Rechenleistung an Bedeutung gewannen.

Recurrent Neural Networks

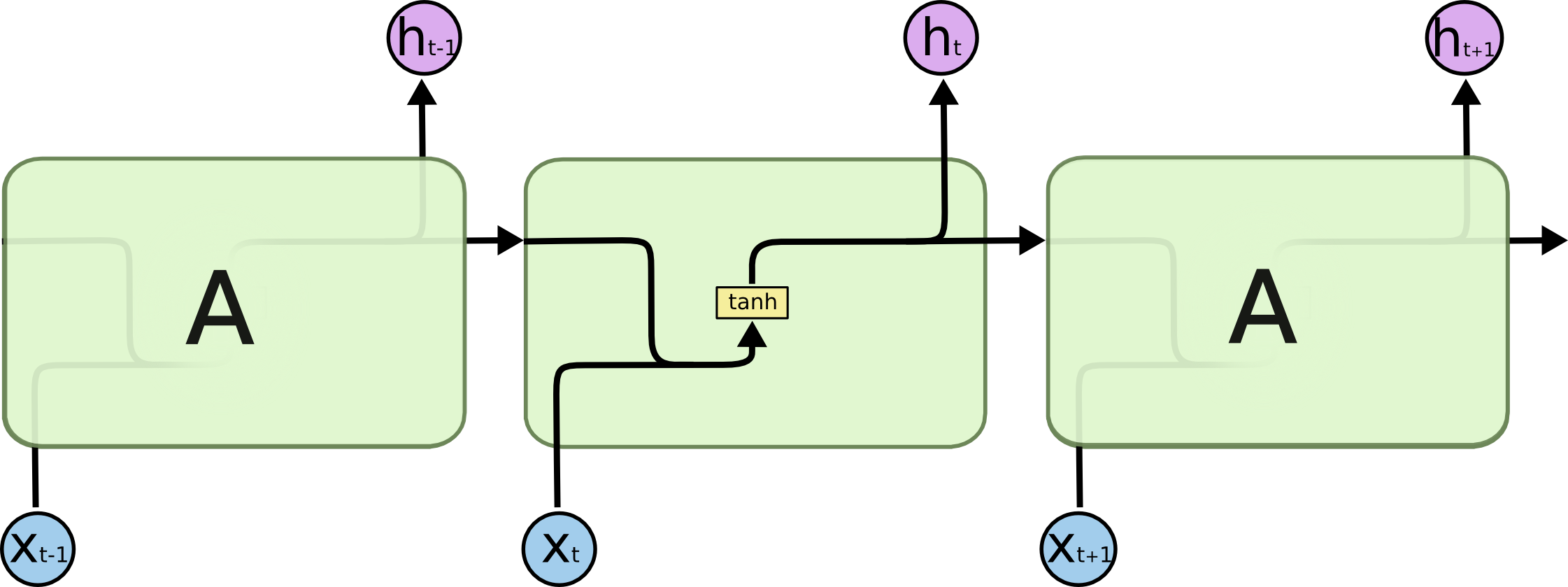
Alle rekurrenten neuronale Netzwerke bilden eine Kette sich wiederholender Module, bestehend aus neuronalen Netzen mit nur einer Schicht.

RNNs (Recurrent Neural Networks) besitzen die Eigenschaft, vorangegange Informationseinheiten im nächsten Lernzyklus zu berücksichtigen. Ein normales RNN ist somit geeignet, sequenzielle Daten zu verarbeiten und in der Findung passender Merkmale für die Ermittlung einer Abbildung der Eingabe- auf die Ausgabedaten einzusetzen. Das fundamentale Problem hier besteht jedoch in dem Verlust von Langzeitinformationen, da mit jedem weiteren rückwärtigen Schritt durch das neuronale Netz zeitlich weit zurückliegende Eingabewerte einen verschwindend geringen Einfluss besitzen. Man kann sich das als eine Art Gedächtnisschwund vorstellen, was RNNs fast in Vergessenheit geraten ließen. Eine Neuerung in der Architektur von RNNs hat das aber verhindert und beinhaltet die Einführung einer LSTM-Einheit (Long Short-Term Memory). LSTMs sind eine spezielle Art von RNNs. Innere kontextuelle Zustandszellen agieren als Langzeit- bzw. Kurzzeitgedächtnis, die die Ausgabe des neuronalen Netzwerks anpassen. Temporale Abhängigkeiten können damit automatisch gelernt werden, da die zeitliche Sequenz als weitere Dimension Eingang findet. Besonders gut für das Verständnis ist das Beispiel anhand eines Filmes. Das aktuelle Bild in einer Szene ist das Ergebnis der vorangegangenen Bilder. Ein LSTM könnte nun unter Verarbeitung des vorangegangenen Abschnittes lernen, welche Informationen für das nächste Bild wichtig sind und welche nicht, und dadurch die Szene extrapolieren. Ein weiteres Beispiel stellt der Wechselkurs in der Finanzwelt dar. Vorangegangene Preismuster werden unter Betrachtung des Währungsverhaltens als Datengrundlage für die weitere Preisentwicklung verwendet.

Bei all den Vorteilen, die ein Deep Learning-Ansatz mit sich bringt, birgt es auch einige Nachteile. In der Regel werden nämlich massive Datenmengen und viele Optimierungszyklen für das Trainieren der neuronalen Netze benötigt. Darüber hinaus gilt auch hier das „No-free-lunch“-Theorem, welches besagt, dass es kein universell gutes Verfahren zur Lösung von Optimierungsproblemen gibt. Damit ist oftmals eine langwierige Justage der Hyperparameter verbunden.

Wenn Sie weitere Informationen zum Thema Deep Learning erhalten wollen oder sich fragen, wie Sie es in Ihrem Unternehmen gewinnbringend einsetzen können, beraten wir Sie gerne!